Modélisation

Grille virtuelle

Maintenant que le décor est en place, on va se pencher sur la manière d'effectuer le rendu de la scène de jeu, avec le serpent et les pommes qui apparaissent aléatoirement.

Ici le rendu est relativement simple. Le « monde » peut être modélisé par une grille sur laquelle sont positionnés les différents objets :

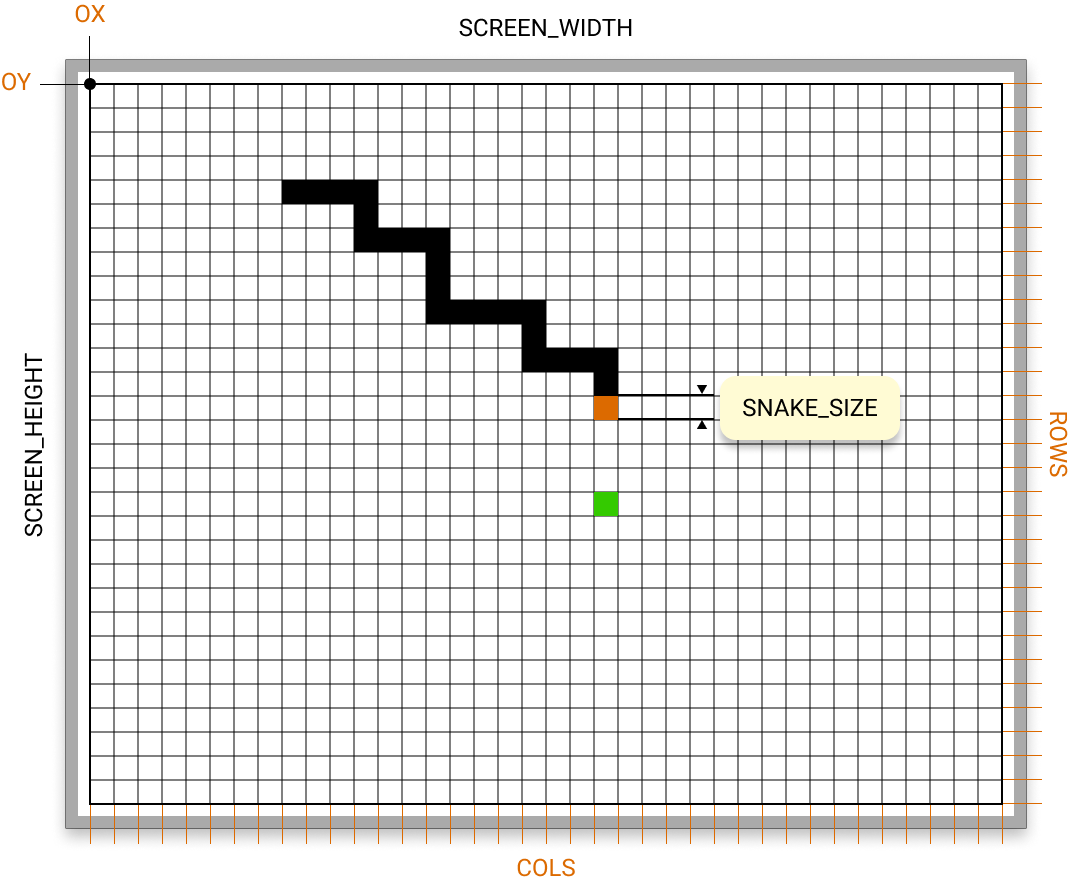
Les cellules de la grille sont carrées et leur taille est déterminée par celle du serpent, ou plus exactement d'un tronçon de serpent. C'est ce que j'ai représenté par le terme SNAKE_SIZE sur le schéma. L'origine de la grille est située aux coordonnées (OX,OY), et la grille comporte COLS colonnes et ROWS lignes.

Tous les tracés que nous allons réaliser dépendent entièrement de ces données. On va donc les déclarer comme des variables globales :

# ----------------------------------------------------------
# Global variables
# ----------------------------------------------------------

SNAKE_SIZE = 2
COLS       = (SCREEN_WIDTH  - 4) // SNAKE_SIZE
ROWS       = (SCREEN_HEIGHT - 4) // SNAKE_SIZE
OX         = (SCREEN_WIDTH  - COLS * SNAKE_SIZE) // 2
OY         = (SCREEN_HEIGHT - ROWS * SNAKE_SIZE) // 2

Le calcul est simple. N'oublie pas que nous avons déjà tracé l'enceinte du terrain qui a 1 pixel d'épaisseur... et on va laisser au moins 1 pixel de distance entre les limites de l'enceinte et celles de la grille. Autrement dit, on retire 2 pixels de chaque côté, horizontalement comme verticalement, de la largeur et de la hauteur de l'écran pour effectuer nos calculs. C'est ce qui explique les termes SCREEN_WIDTH - 4 et SCREEN_HEIGHT - 4.

L'opérateur // applique une division entière. Le résultat de cette division correspond simplement à la partie entière du quotient.

Le serpent

Comment va-t-on modéliser le serpent ? Pour le déterminer, penchons-nous un peu sur la manière dont il se déplace sur la grille du monde.

Modélisation

À chaque instant t, le serpent progresse d'une cellule dans la direction que lui impose le joueur par l'intermédiaire du PAD directionnel de la console. Et pour modéliser le corps tout entier du serpent, on a besoin de mémoriser la succession des cellules par lesquelles la tête est passée aux instants antérieurs à t. La longueur de la séquence mémorisée correspond à la longueur du serpent :

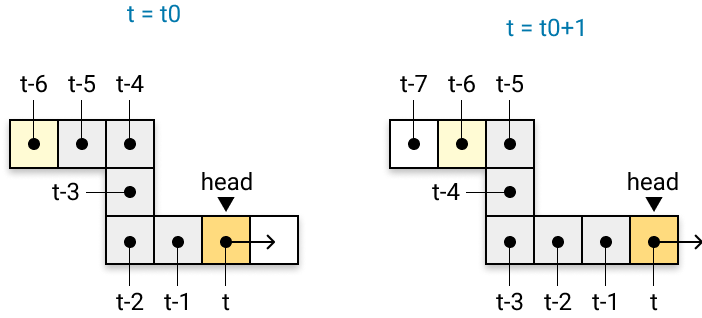
À chaque fois que le serpent progresse d'une cellule, il va donc falloir mémoriser deux données : l'abscisse x et l'ordonnée y de la tête du serpent. Mais il faudra également conserver les anciennes positions qu'elle occupait, aux instants antérieurs.

Pour cela, on va utiliser une structure de données qu'on appelle une « liste » en Python (qui pourrait s'apparenter à un tableau dynamique, qu'on trouve dans d'autres langages). En effet, la structure dont on a besoin doit être de taille dynamique, puisqu'à chaque fois que le serpent avale une pomme, elle doit pouvoir s'allonger... Une liste fera donc parfaitement l'affaire, puisqu'il s'agit précisément d'une structure de données dynamique.

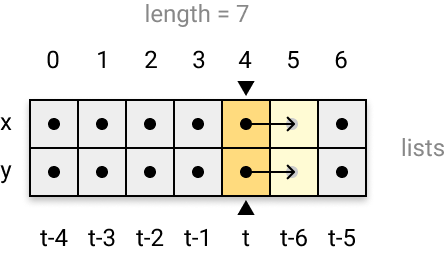
Chaque élément de la liste est repéré par un index allant de 0 à n-1 (où n correspond à la longueur de la liste). Par conséquent, si la longueur du serpent est 7 (comme sur le schéma ci-dessus), les positions successives occupées par la tête du serpent aux instants t, t-1, t-2, t-3, t-4, t-5 et t-6 seront enregistrées dans deux listes distinctes x et y, et associées aux index compris entre 0 et 6.

Le principe d'enregistrement des positions est simple. Il suffit d'associer aux listes x et y un curseur, qu'on pourrait assimiler à une tête de lecture, qui désigne la position de la tête du serpent. À chaque fois que le serpent progresse d'une cellule, on déplace la tête de lecture d'une case vers la droite dans la liste, et on enregistre la nouvelle position de la tête du serpent. En faisant cela, on écrase simplement la position qu'elle occupait à l'instant t-7, dont on n'a plus besoin, dans la mesure où on ne conserve ses positions que jusqu'à l'instant t-6.

Lorsque la tête de lecture est positionnée sur le dernier index de la liste, le prochain enregistrement est effectué en ramenant la tête de lecture au début de la liste (à l'index 0). Le processus est donc cyclique car il effectue finalement des « rotations » sur les listes. Tout se passe comme si les listes étaient enroulées comme des anneaux. de serpent 

Voyons un peu comment mettre ça en œuvre avec Python.

Implémentation

Soit la liste l définie par :

l  = [1, 2, 4, 8, 16, 32, 64, 128, 256]

L'élément d'indice 4 s'obtient avec :

l[4] # --> renvoie la valeur du cinquième élément : 16

Pour enregistrer la valeur 'sixteen' à l'indice 4, on écrira :

l[4] = 'sixteen'

# --> la liste devient [1, 2, 4, 8, 'sixteen', 32, 64, 128, 256]

Tu vois qu'on peut aussi mélanger les types de données sans problème dans une liste.

Python propose également une structure de données assez proche de la liste, dans laquelle les éléments enregistrés ne sont pas nécessairement indexés par des entiers, mais par des clefs alphanumériques. Cette structure s'appelle un dictionnaire :

d = {
    'head': 4,
    'x':    [0, 1, 2, 2, 2, 3, 4, 5],
    'y':    [0, 0, 0, 1, 2, 2, 2, 2]
}

Tiens, tiens... ça ressemble à la manière dont on pourrait implémenter notre serpent ça !    Tu vois que la valeur associée à une clef peut tout à fait être une liste. On pourrait même imbriquer un dictionnaire dans un dictionnaire... ou encore, construire des listes de dictionnaires, qui imbriqueraient eux-mêmes des listes... La structuration des données peut devenir complexe. Nous nous limiterons à des structures simples dans le cadre de cet atelier. Et n'oublie pas que ces structures de données sont hébergées dans la mémoire vive de la console. Donc, il est judicieux de choisir des structures de données qui ne consomment pas plus de mémoire que nécessaire.

Les dictionnaires permettent aussi de définir des structures de données composites selon lesquelles une variable peut être décrite par plusieurs propriétés. Dans l'exemple ci-dessus, la variable d est décrite par les proprietés head, x et y. Ce procédé permet ainsi de définir des sortes de « super-variables », c'est-à-dire des variables qui agrègent elles-mêmes plusieurs variables. Ça ressemble (de loin) aux struct du langage C. Sauf qu'un struct n'est pas une structure dynamique, alors que les dictionnaires de Python le sont.

Pour accéder à la valeur associée à la clef head dans le dictionnaire d, on écrira simplement :

d['head'] # --> retourne la valeur 4

Et pour affecter la valeur 5 à cette même clef, on écrira :

d['head'] = 5

Simple, nan ?

Allez, j'crois qu'on a assez d'éléments pour avancer.
Modélisons notre serpent :

# ----------------------------------------------------------
# Initialization
# ----------------------------------------------------------

snake = {
    'x':    [],
    'y':    [],
    'head': 0,
    'len':  0,
    'vx':   0,
    'vy':   0
}

On retrouve bien les listes de coordonnées x et y, qui sont vides pour le moment. La propriété head désigne la position de la tête de lecture dans les listes x et y. Bien que Python propose une fonction len() qui permet de calculer la longueur d'une liste, pour des raisons d'optimisation j'ai préféré ajouter une propriété len à la structure snake pour stocker la longueur des listes x et y. Enfin, j'ai ajouté deux propriétés vx et vy qui représentent les composantes horizontale et verticale de la vitesse de déplacement du serpent sur la grille.

La structure de données représentant notre serpent est maintenant initialisée. À chaque nouvelle partie, ses propriétés seront systématiquement réinitialisées à des valeurs par défaut. Aussi je te propose qu'on décrive cette procédure de réinitialisation dans une fonction resetSnake() :

# ----------------------------------------------------------
# Snake management
# ----------------------------------------------------------

def resetSnake():
    x = COLS // 2
    y = ROWS // 2
    snake['x'] = []
    snake['y'] = []
    for _ in range(SNAKE_LENGTH):
        snake['x'].append(x)
        snake['y'].append(y)
    snake['head'] = SNAKE_LENGTH - 1
    snake['len']  = SNAKE_LENGTH
    snake['vx'] = 0
    snake['vy'] = 0

On commence par calculer les coordonnées de départ x et y du serpent. Il est ici positionné au centre de la grille :

x = COLS // 2
y = ROWS // 2

Les listes snake['x'] et snake['y'] sont réinitialisées par des listes vides :

snake['x'] = []
snake['y'] = []

Puis on va les remplir avec les coordonnées x et y qu'on vient juste de calculer. J'introduis ici une nouvelle variable globale qui désigne la longueur initiale du serpent SNAKE_LENGTH, et qu'on va tout de suite définir :

# ----------------------------------------------------------
# Global variables
# ----------------------------------------------------------

SNAKE_LENGTH = 4

La boucle for se lit simplement : elle incrémente un itérateur anonyme _ dans l'intervalle [0, SNAKE_LENGTH - 1] et exécute, à chaque itération, les instructions qu'elle encapsule :

for _ in range(SNAKE_LENGTH):
    snake['x'].append(x)
    snake['y'].append(y)

Ceci a pour effet d'ajouter :

• la valeur de x à la fin de la liste snake['x']
• la valeur de y à la fin de la liste snake['y']

Et comme on répète ces opérations SNAKE_LENGTH fois (c'est-à-dire 4 fois), lorsque la boucle se termine les listes sont ainsi définies :

  0   1   2   3

[19, 19, 19, 19]    snake['x']
[15, 15, 15, 15]    snake['y']

              ^
             head

En effet, au départ tous les tronçons du serpent sont rassemblés sur la même cellule (comme si le serpent était enroulé sur lui-même).

La tête de lecture des listes est positionnée à l'indice SNAKE_LENGTH - 1 (donc 3), c'est l'indice des coordonnées de la tête du serpent.

La longeur du serpent est initialisée à SNAKE_LENGTH (donc 4), et la vitesse initiale du serpent est nulle (il ne se déplace pas encore).

snake['head'] = SNAKE_LENGTH - 1
snake['len']  = SNAKE_LENGTH
snake['vx'] = 0
snake['vy'] = 0

À partir d'ici, notre serpent est dans la matrice... on ne le voit pas encore, parce-qu'on n'a pas encore écrit la routine d'affichage qui nous permette de l'observer. On ne peut pas non plus lui transmettre de commandes pour qu'il se déplace.

Mais c'est justement ce qu'on va faire à la prochaine étape !