Modeling
Step 3
Modeling a virtual world.
Snake modeling.
Implementation using lists and dictionaries.
The virtual grid
Now that the scenery is in place, we will look at how to render the game scene, with the snake and apples appearing randomly.
Here the rendering is relatively simple. The "world" can be modeled by a grid on which the different objects are positioned:
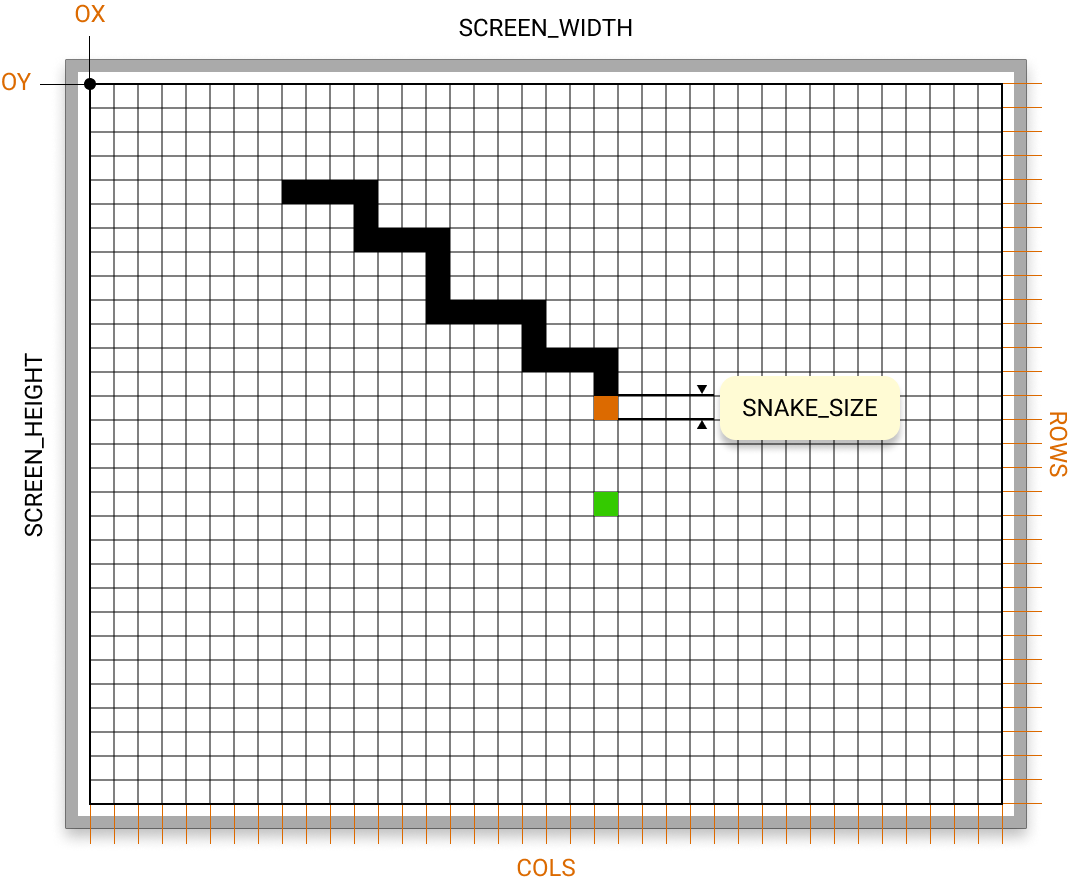
The grid cells are square and their size is determined by the size of the snake, or more precisely of a section of snake. This is what I represented by the term SNAKE_SIZE in the diagram. The origin of the grid is located at the (OX,OY) coordinates, and the grid contains COLS columns and ROWS rows.
All the plots we are going to make depend entirely on this data. We will therefore declare them as global variables:
# ----------------------------------------------------------
# Global variables
# ----------------------------------------------------------
SNAKE_SIZE = 2
COLS = (SCREEN_WIDTH - 4) // SNAKE_SIZE
ROWS = (SCREEN_HEIGHT - 4) // SNAKE_SIZE
OX = (SCREEN_WIDTH - COLS * SNAKE_SIZE) // 2
OY = (SCREEN_HEIGHT - ROWS * SNAKE_SIZE) // 2
The calculation is simple. Don't forget that we have already plotted the ground enclosure which is 1 pixel thick... and we will leave at least 1 pixel of distance between the boundaries of the enclosure and those of the grid. In other words, we remove 2 pixels on each side, horizontally and vertically, from the width and height of the screen to perform our calculations. This explains the terms SCREEN_WIDTH - 4 and SCREEN_HEIGHT - 4.
The // operator is an integer division. The result of this division simply corresponds to the integer part of the quotient.
The snake
How are we going to model the snake? To determine this, let's take a look at how it moves on the virtual grid.
Modeling
At each t time, the snake advances from a cell in the direction imposed by the player through the console's directional PAD. And to model the entire body of the snake, we need to memorize the succession of cells through which the head passed at times prior to t. The length of the stored sequence corresponds to the length of the snake:

Each time the snake advances from a cell, it will therefore be necessary to memorize two data: the x abscissa and the y ordinate of the snake's head. But it will also be necessary to maintain the former positions she held in the previous moments.
To do this, we will use a data structure called a "list" in Python (which could be similar to a dynamic table, found in other languages). Indeed, the structure we need must be of dynamic size, since each time the snake swallows an apple, it must be able to lengthen... A list will therefore do just fine, since it is precisely a dynamic data structure.
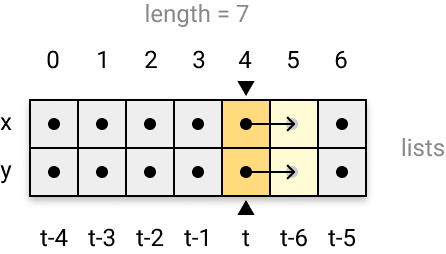
Each item in the list is identified by an index ranging from 0 to n-1 (where n corresponds to the length of the list). Therefore, if the length of the snake is 7 (as shown in the diagram above), the successive positions occupied by the snake head at times t, t-1, t-2, t-3, t-4, t-5 and t-6 will be recorded in two separate lists x and y, and associated with the indexes between 0 and 6.
The position recording procedure is simple. It is enough to associate to the lists x and y a cursor, which could be assimilated to a reading head, which indicates the position of the snake's head. Each time the snake moves one cell forward, the reading head is moved one box to the right in the list, and the new position of the snake's head is recorded. By doing this, we simply overwrite the position it occupied at the time t-7, which is no longer needed, as long as we only keep its positions until the time t-6.
When the reading head is positioned on the last index of the list, the next recording is made by bringing the reading head back to the beginning of the list (to the 0 index). The process is therefore cyclical because it finally "rotates" on the lists. Everything happens as if the lists were rolled up like snake rings.
Let's see how to implement this with Python.
Implementation
Let the l list be defined by :
l = [1, 2, 4, 8, 16, 32, 64, 128, 256]
The element of index 4 is obtained with:
l[4] # --> returns the value of the fifth element: 16
To store the value 'sixteen'' at index4', write:
l[4] = 'sixteen'
# --> the list becomes [1, 2, 4, 8, 'sixteen', 32, 64, 128, 256]
You see that you can also mix the types of data in a list, without any problem.
Python also offers a data structure quite close to the list, in which the recorded elements are not necessarily indexed by integers, but by alphanumeric keys. This structure is called a dictionary:
d = {
'head': 4,
'x': [0, 1, 2, 2, 2, 3, 4, 5],
'y': [0, 0, 0, 1, 2, 2, 2, 2]
}
Well... it looks like the way we could implement our snake! You see that the value associated with a key can be a list. We could even nest a dictionary in a dictionary... or even build lists of dictionaries, which would themselves nest lists... Data structuring can become complex. We will limit ourselves to simple structures in this workshop. And don't forget that these data structures are hosted in the console's RAM. Therefore, it is wise to choose data structures that do not consume more memory than necessary.
Dictionaries also make it possible to define composite data structures according to which a variable can be described by several properties. In the example above, the variable d is described by head, x and y properties. This process thus makes it possible to define kinds of "super-variables", i.e. variables that themselves aggregate several variables. It looks (by far) like the struct of the C language. Except that a struct is not a dynamic structure, whereas Python dictionaries are.
To access the value associated with the head key in the d dictionary, simply write:
d['head'] # --> returns 4
And to assign the value 5 to this same key, we will write :
d['head'] = 5
Simple, right?
Come on, I think we have enough to move forward.
Let's model our snake:
# ----------------------------------------------------------
# Initialization
# ----------------------------------------------------------
snake = {
'x': [],
'y': [],
'head': 0,
'len': 0,
'vx': 0,
'vy': 0
}
We can see the lists of coordinates x and y, which are empty for the moment. The head property refers to the position of the reading head in the x and y lists. Although Python offers a len() function that allows you to calculate the length of a list, for optimization reasons I preferred to add a len property to the snake structure to store the length of the x and y lists. Finally, I added two properties vx and vy which represent the horizontal and vertical components of the velocity of the snake's movement on the grid.
The data structure representing our snake is now initialized. With each new game, its properties will be systematically reset to default values. So I suggest that we describe this reset procedure in a resetSnake() function:
# ----------------------------------------------------------
# Snake management
# ----------------------------------------------------------
def resetSnake():
x = COLS // 2
y = ROWS // 2
snake['x'] = []
snake['y'] = []
for _ in range(SNAKE_LENGTH):
snake['x'].append(x)
snake['y'].append(y)
snake['head'] = SNAKE_LENGTH - 1
snake['len'] = SNAKE_LENGTH
snake['vx'] = 0
snake['vy'] = 0
First we calculate the starting coordinates x and y of the snake. It is positioned here in the center of the grid:
x = COLS // 2
y = ROWS // 2
The snake['x'] and snake['y'] lists are reset by empty lists:
snake['x'] = []
snake['y'] = []
Then we will fill them with the x and y coordinates that we have just calculated. I introduce here a new global variable that designates the initial length of the snake SNAKE_LENGTH, and that we will immediately define:
# ----------------------------------------------------------
# Global variables
# ----------------------------------------------------------
SNAKE_LENGTH = 4
The for loop increments an anonymous iterator _ in the interval [0, SNAKE_LENGTH - 1] and executes, at each iteration, the nested instructions:
for _ in range(SNAKE_LENGTH):
snake['x'].append(x)
snake['y'].append(y)
This has the effect of adding:
- the
xvalue at the end of thesnake['x']list - the
yvalue at the end of thesnake['y']list
And as we repeat these operations SNAKE_LENGTH times (i.e. `4 times), when the loop ends the lists are defined as follows:
0 1 2 3
[19, 19, 19, 19] snake['x']
[15, 15, 15, 15] snake['y']
^
head
Indeed, at the beginning all the sections of the snake are gathered on the same cell (as if the snake were wrapped around itself).
The list reading head is positioned at the index SNAKE_LENGTH - 1 (therefore 3), it is the index of the coordinates of the snake head.
The length of the snake is initialized to SNAKE_LENGTH (therefore 4), and the initial velocity of the snake is zero (it does not yet move).
snake['head'] = SNAKE_LENGTH - 1
snake['len'] = SNAKE_LENGTH
snake['vx'] = 0
snake['vy'] = 0
From here, our snake is in the matrix... we don't see it yet, because we haven't written the display routine that allows us to observe it yet. Nor can we apply him commands to move around.
But that's exactly what we're going to do in the next step!